Xác định thông số động học của quá trình nitrit hoá bán phần/ anammox nhằm loại bỏ amoni trong nước thải sinh hoạt

1. Mở đầu

Cùng với sự phát triển của xã hội, lượng nước thải sinh hoạt ngày càng gia tăng đặt ra những thách thức đối với môi trường. Với mức độ đô thị hóa như hiện nay, đến năm 2035 Việt Nam sẽ có khoảng 106,3 triệu người, trong đó 47,87 triệu dân thành thị (44,87% dân số) [2]. Lượng nước thải cần xử lý ước tính lên tới 7,63 triệu m3/ngđ. Để tránh ảnh hưởng đến sức khỏe cộng đồng và môi trường, cùng với việc xử lý các chất hữu cơ trong nước thải, thông số nitơ cũng cần được kiểm soát theo Quy chuẩn kỹ thuật quốc gia về nước thải sinh hoạt QCVN 14:2008/BTNMT. Nồng độ xả cho phép của nitơ amoni đối với nguồn nước loại A và loại B lần lượt là 5 mg/L và 10 mg/L. Một số công nghệ loại bỏ nitơ hiện nay dựa trên quá trình nitrat hóa/khử nitrat còn nhiều nhược điểm cần khắc phục như tiêu tốn nhiều năng lượng, cần tuần hoàn bùn bên trong, cần bổ sung nguồn carbon hữu cơ v.v.. [6].

Quá trình oxy hóa kỵ khí amoni (Anammox) lần đầu tiên được phát hiện tại nhà máy xử lý nước thải Gist Brocades ở Hà Lan vào năm 1995 [8] và những năm sau đó, nhiều nghiên cứu trên thế giới đã chứng minh nó có nhiều ưu điểm. Cụ thể, quá trình Anammox có hiệu suất cao và chi phí vận hành thấp do không cần bổ sung nguồn carbon bên ngoài , tiết kiệm năng lượng sục khí, tạo ra rất ít bùn, tiết kiệm chi phí xử lý bùn, giảm phát thải khí nhà kính và tiết kiệm diện tích xây dựng. Vì vậy, công nghệ anammox đã được nghiên cứu thành công ở quy mô phòng thí nghiệm, quy mô thí điểm và/hoặc quy mô đầy đủ được coi là giải pháp đầy triển vọng để xử lý nước thải giàu amoni. Tuy nhiên, quá trình anammox vẫn còn một số hạn chế do tốc độ phát triển của vi khuẩn anammox thấp, nhạy cảm với những thay đổi của điều kiện môi trường, v.v [9]. Hiệu suất loại bỏ amoni của quá trình anammox sẽ khác nhau giữa nghiên cứu về các loại nước thải khác nhau, mô hình phản ứng và các điều kiện vận hành khác nhau. Cùng với việc xác định mô hình động học phù hợp, hiệu quả xử lý và giá trị nước thải đầu ra cũng có thể được dự đoán được.

Để áp dụng công nghệ xử lý nitơ bằng quy trình Anammox cần tiến hành đánh giá lâu dài hiệu quả xử lý, xác định các điều kiện vận hành tối ưu miễn là mô hình động học phù hợp. Do đó, hệ thống nitrit hóa bán phần/anammox (PN/AX) sử dụng chất mang sinh khối cố định trong 210 ngày đã được nghiên cứu để đánh giá hiệu quả lâu dài của việc xử lý nitơ trong nước thải sinh hoạt và các hằng số động học của mô hình phù hợp nhất cũng được xác định trong nghiên cứu này.

2. Cơ sở lý thuyết của động học phản ứng

Động học quá trình xử lý sinh học liên quan đến quá trình phân huỷ cơ chất, quá trình sinh trưởng tế bào và quá trình phân huỷ nội bào. Tốc độ của phản ứng được xác định bằng phương trình (1):

Mối liên hệ giữa tốc độ phản ứng, nồng độ cơ chất và bậc của phản ứng được biểu diễn qua phương trình (2):

Trong đó:

r: tốc độ phản ứng (mg/L/ngày)

S: nồng độ cơ chất (mg/L)

t: thời gian phản ứng hoặc thời gian lưu thủy lực HRT (ngày)

k: hằng số tốc độ phản ứng (ngày^-1)

n: bậc phản ứng (n = 0,1,2,…n)

Từ phương trình (1) và (2), ta có được:

Một biểu thức khác được sử dụng để mô tả tốc độ liên quan đến xử lý nước thải sinh học dựa trên các phản ứng enzym, mà động học của chúng được đề xuất bởi Michaelis và Menten:

Trong đó:

r_max: tốc độ phản ứng tối đa (mg/L/ngày)

S: nồng độ cơ chất (mg/L)

K_S: hằng số bán bão hoà (mg/L)

Động học quá trình liên quan đến các yếu tố vận hành và môi trường ảnh hưởng đến tỷ lệ sử dụng chất nền. Trong mô hình phản ứng, cân bằng vật chất được xác định theo phương trình sau:

Hay có thể viết dưới dạng:

Tuy nhiên, do thể tích của mô hình phản ứng là không đổi nên dV/dt=0 nên phương trình (6) được viết lại như sau:

Trong đó:

Q: lưu lượng dòng (L/ngày)

V: thể tích mô hình (L)

S₀: nồng độ cơ chất đầu vào (mg/L)

S_e: nồng độ cơ chất đầu ra (mg/L)

Khi mô hình ở trạng thái ổn định thì tốc độ phản ứng được xác định theo công thức sau:

a. Phương trình động học bậc 1

Phương trình động học được xây dựng trên cơ sở giả định phương trình động học bậc 1 trong mô hình là chiếm ưu thế và các cơ chất trong mô hình được khuấy trộn đều [5]. Khi đó phương trình động học bậc 1 được biểu diễn:

trong đó:

K₁: hằng số tốc độ loại bỏ cơ chất của mô hình động học bậc một (ngày^-1)

Phương trình (11) được biểu diễn dưới phương trình tuyến tính dạng y = k.x. Hằng số tốc độ loại bỏ cơ chất bậc một k₁ được xác định bằng độ dốc k của đồ thị thể hiện mối quan hệ giữa (S₀-S_e)/HRT (trục tung) và S_e (trục hoành).

b. Phương trình động học bậc 2 Grau

Sự biến thiên nồng độ cơ chất được biểu diễn qua phương trình động học bậc 2 Grau [3]:

Tích phân hai vế phương trình (13) ta có:

trong đó:

k₂: hằng số tốc độ loại bỏ cơ chất của mô hình động học bậc hai (ngày^-1)

X: tổng nồng độ sinh khối trong mô hình (mg/L)

Trong quá trình Anammox, lượng sinh khối tạo thành rất ít, coi như không thay đổi nên: . Đặt giá trị và đưa phương trình (14) về dạng phương trình tuyến tính y = a.x + b với HRT là biến số x và HRT/E là hàm phụ thuộc y. Khi đó phương trình toán mô tả động học bậc hai Grau được biểu diễn như sau:

Hằng số tốc độ loại bỏ cơ chất của mô hình động học bậc hai được xác định theo công thức sau:

c. Phương trình động học Stover-Kincannon

Phương trình động học Stover-Kincannon là phương trình toán được sử dụng phổ biến để xác định tốc độ loại bỏ cơ chất và được thể hiện bằng phương trình sau [17]:

Trong đó:

K_B: hằng số bán bão hoà (mg/L/ngày)

U_max: tốc độ tiêu thụ cơ chất lớn nhất (mg/L/ngày)

Nghịch đảo phương trình (17), ta có thể được viết thành:

Ta có: và . Phương trình (18) được đưa về dạng tuyến tính y = c.x + d viết dưới dạng:

Khi đó, tốc độ tiêu thụ cơ chất lớn nhất U_max=1/d và hằng số bán bão hòa K_B=c/d với các giá trị c, d được xác định từ đồ thị thể hiện mối liên hệ giữa HRT/(S₀-S_e) (trục tung) và HRT/S₀ (trục hoành).

3. Thí nghiệm xác định động học của quá trình nitrit hoá bán phần và Anammox nhằm loại bỏ amoni trong nước thải sinh hoạt

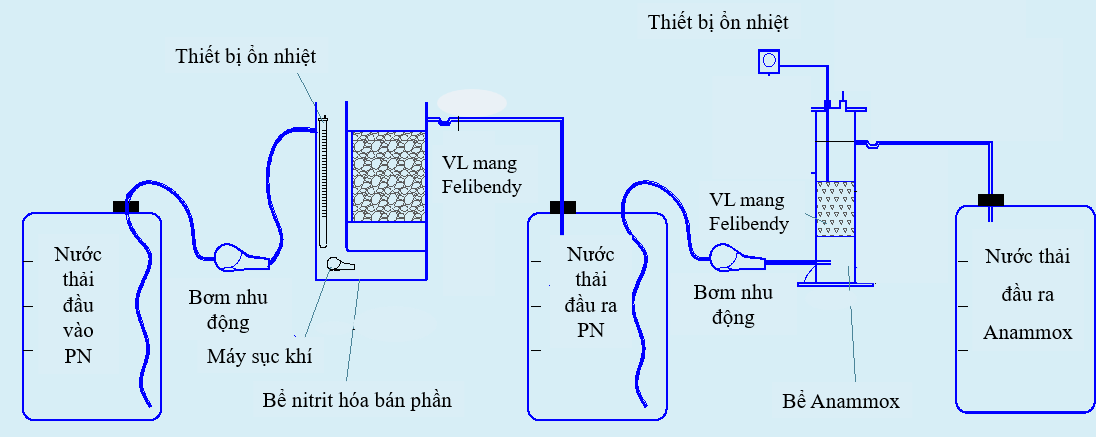
Để loại bỏ amoni trong nước thải sinh hoạt, một hệ mô hình PN/AX thực hiện quá trình nitrit hoá bán phần/anammox đã được thiết lập. Mô hình thí nghiệm được mô tả trong hình 1.

Hệ mô hình PN/AX gồm 2 mô hình PN và AX nối tiếp nhau, trong đó nước thải đầu ra của mô hình PN là nước thải đầu vào của mô hình AX. Trong mô hình PN, các vi khuẩn Nitrosomonas sẽ tiến hành quá trình oxi chuyển hoá một phần amoni thành nitrit, tạo tỉ lệ NO₂^--N/NH₄⁺-N ≈ 1:1 là tiền đề thích hợp cho phản ứng Anammox tiếp theo diễn ra. Trong mô hình AX, các vi sinh vật Planctomycetes bám giá thể sử dụng nitrit trong nước thải là chất nhận điện tử, amoni là chất nhường điện tử và tiến hành quá trình oxi hoá kỵ khí amoni thành khí nitơ. Vật liệu mang Felibendy (sản phẩm của công ty Kurarray, Nhật Bản) được sử dụng làm giá thể cho vi sinh vật dính bám trong hệ mô hình PN/AX.

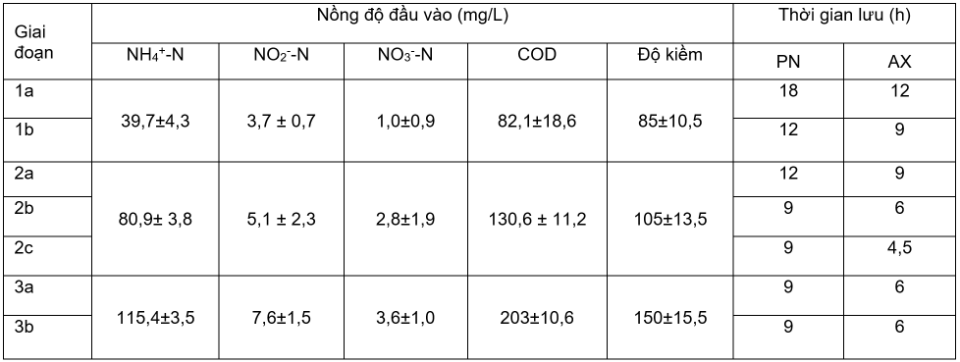
Nghiên cứu được tiến hành trong thời gian 210 ngày được chia thành 3 giai đoạn: giai đoạn 1 (1a, 1b), giai đoạn 2 (2a, 2b, 2c) và giai đoạn 3 (3a, 3b) sử dụng nước thải sinh hoạt (nước thải nhân tạo) có thành phần như trong bảng 1.

Bảng 1. Thành phần nước thải trong thí nghiệm

4. Kết quả nghiên cứu

Kết quả thực nghiệm cho thấy, sau 210 ngày thí nghiệm với nước thải sinh hoạt, hiệu suất loại bỏ amoni và tổng nitơ của hệ thống PN/AX đạt lần lượt 91,4% và 69,8%. Chất lượng nước thải đầu ra đạt yêu cầu theo QCVN 14:2008/BTNMT (cột B).

Để mô tả động học của quá trình nitrat hóa một phần và Anammox, nghiên cứu đã sử dụng ba phương trình động học thường được sử dụng: bậc một, bậc hai Grau và mô hình Stover Kincannon. Dữ liệu đầu vào cho tất cả các mô hình động học này phải ở trạng thái ổn định của hệ phản ứng. Từ các số liệu được phân tích trong thí nghiệm như nồng độ cơ chất nước đầu vào (S0), nồng độ cơ chất nước thải (Se), thời gian lưu thủy lực (HRT), thể tích bể phản ứng (V), tốc độ dòng chảy (Q), hiệu suất xử lý (E) thiết lập mối quan hệ tương quan giữa các tham số của phương trình động học. Bằng phần mềm Microsoft Excel, thiết lập các phương trình tuyến tính mô tả quá trình động học và được thể hiện trên Hình 2 (đối với quá trình nitrit hóa bán phần) và Hình 3 (đối với quá trình Anammox).

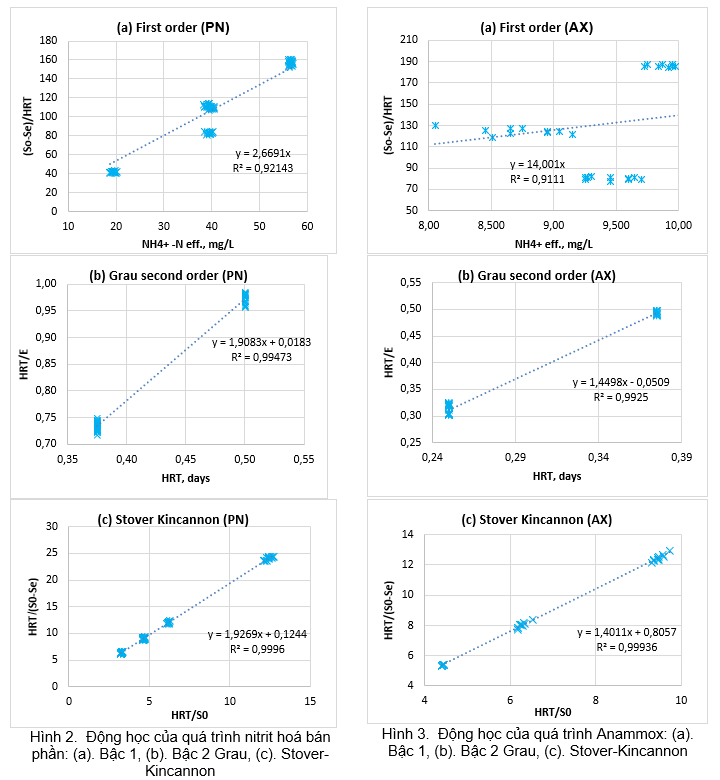
Số liệu thực nghiệm trong mô hình PN và mô hình AX được áp dụng cho động học loại bỏ chất nền bậc nhất để xác định tốc độ thay đổi nồng độ amoni như trong Hình 2a và Hình 3a. Hằng số bậc một (K₁) của quá trình nitrat hóa một phần và anammox thu được bằng cách vẽ đồ thị (S₀ −S_e )/HRT so với (S_e ) là 2,66 và 14,001 mỗi ngày đối với tốc độ loại bỏ amoni với R² lần lượt là 0,921 và 0,911.

Bằng cách vẽ đồ thị HRT so với HRT/E, các hệ số động học của mô hình bậc hai Grau được xác định dựa trên độ dốc và giao điểm của đồ thị trong Hình 2b và Hình 3b. Hệ số xác định R² của mô hình bậc hai Grau là 0,994 đối với quá trình nitrat hóa một phần và là 0,992 đối với quá trình anammox, cao hơn mô hình bậc một. Giá trị của a và b đối với quá trình nitrat hóa một phần được tính tương ứng là 1,908 và 0,018. Giá trị của a và b cho quá trình Anammox được xác định lần lượt là 1,449 và 0,051.

Số liệu thực nghiệm trong lò phản ứng PN và lò phản ứng AX cũng được áp dụng cho động học loại bỏ chất nền Stover Kincannon để xác định tốc độ thay đổi nồng độ amoni như trong Hình 2c và Hình 3c. Bằng cách vẽ đồ thị HRT/(S0-Se) so với HRT/S0, hệ số xác định R2 của mô hình Stover Kincannon là 0,999 cho cả quá trình nitrat hóa một phần và quá trình anammox, là giá trị cao nhất trong số ba mô hình được trình bày. Giá trị KB và Umax cho quá trình nitrat hóa một phần được tính tương ứng là 15,489 và 8,038. Giá trị KB và Umax cho quá trình nitrat hóa một phần được tính tương ứng là 1,738 và 1,241.

Từ các phương trình tuyến tính được thiết lập trong Hình 3 và 6, các hằng số động học của mô hình bậc một, bậc hai Grau và mô hình Stover Kincannon được xác định và trình bày trong Bảng 2.

Bảng 2. Thông số động học của một số nghiên cứu khác

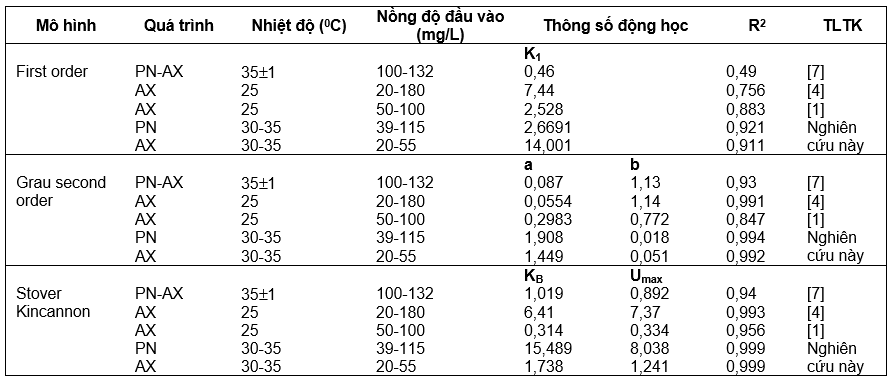
Kết quả nghiên cứu này có sự tương đồng với các nghiên cứu trước đây. Sự khác biệt giữa các hằng số động học của nghiên cứu này và các nghiên cứu khác được trình bày trong Bảng 3 có thể là do tốc độ nạp nitơ được áp dụng và đặc tính nước thải được sử dụng. Nó cũng có thể là do sự khác biệt về cấu hình của mô hình phản ứng sinh học, thể tích hiệu dụng (V), tốc độ dòng chảy (Q) và các điều kiện vận hành như nhiệt độ và nồng độ dòng vào. Trong bậc một là mô hình Grau và Stover Kincannon, mô hình Stover-Kincannon có hệ số động học R² cao nhất. Điều đó có nghĩa là độ phân tán của dữ liệu thu được trong Stover Kincannon cao hơn so với mô hình cấp một và cấp hai Grau. Nhiều nghiên cứu trên thế giới cũng đã khẳng định nhận rằng Stover–Kincannon cải tiến có tính ứng dụng cao hơn các mô hình động học loại bỏ amoni được đề cập khác. Do đó, nồng độ amoni trong nước thải của quá trình nitrat hóa bán phần và anammox trong hệ mô hình PN/AX của nghiên cứu này có thể được dự đoán bằng mô hình động học Stover Kincannon được biểu diễn qua phương trình (9), (10):

Quá trình nitrit hoá bán phần:

Quá trình Anammox:

5. Kết luận

Hệ thống PN/AX sử dụng vật liệu mang Felibendy đã được sử dụng để nghiên cứu loại bỏ amoni trong nước thải sinh hoạt. Hiệu suất loại bỏ amoni là 91,4% sau 210 ngày vận hành. Trên cơ sở ba mô hình động học cơ bản (mô hình động học bậc 1, bậc 2 Grau và mô hình Stover Kincannon), nghiên cứu đã xác định được mô hình phù hợp nhất để mô tả động học của quá trình nitrit hoá bán phần/anammox nhằm loại bỏ amoni trong nước thải sinh hoạt là mô hình Stover Kincannon. Nghiên cứu cũng đã xác định được các thông số động học của mô hình Stover Kincannon và dự đoán được nồng độ amoni trong nước thải đầu ra của quá trình xử lý của mô hình này.

TÀI LIỆU THAM KHẢO

Abyar, H., Younesi, H., Bahramifar, N., Zinatizadeh, A. A., & Amini, M. (2017). Kinetic evaluation and process analysis of COD and nitrogen removal in UAASB bioreactor. Journal of the Taiwan institute of chemical engineers, 78, 272-281. https://doi.org/10.1016/j.jtice.2017.06.014
Cao Thế Hà, Vũ Ngọc Duy, Nguyễn Thị An Hằng, Nguyễn Trường Quân, Trần Mạnh Hải (2019), “Hiện trạng công nghệ xử lý nước thải theo hướng phát triển bền vững”, Tạp chí Khoa học và Công nghệ Việt Nam, (1B), 50.
Grau, P., Dohanyos, M., & Chudoba, J. (1975). Kinetics of multicomponent substrate removal by activated sludge.Water Research, 9(7), 637-642. https://doi.org/10.1016/0043-1354(75)90169-4
Huang, X. W., Wei, Q. Y., Urata, K., Tomoshige, Y., Zhang, X. H., & Kawagoshi, Y. (2014). Kinetic study on nitrogen removal performance in marine anammox bacterial culture. Journal of bioscience and bioengineering, 117(3), 285-291. https://doi.org/10.1016/j.jbiosc.2013.08.004
Jin, R. C., Yang, G. F., Yu, J. J., & Zheng, P. (2012). The inhibition of the Anammox process: a review.Chemical engineering journal, 197, 67-79. https://doi.org/10.1016/j.cej.2012.05.014
Ngân hàng Thế giới (2013), Báo cáo Đánh giá hoạt động quản lý nước thải đô thị tại Việt Nam.
Niu Q, Zhang Y, Ma H, He S, Li Y-Y (2016). Reactor kinetics evaluation and perfor- mance investigation of a long-term operated UASB-anammox mixed culture process. Int Biodeterior Biodegrad, 108:24–33. https://doi.org/10.1016/j.ibiod.2015.11.024
Mulder, A., van de Graaf, A.A., Robertson, L.A., Kuenen, J.G. (1995). Anaerobic ammonium oxidation discovered in a denitrifying fluidized bed reactor. FEMS Microbiol. Ecol. 16 (3), 177–184. https://doi.org/10.1111/j.1574-6941.1995.tb00281.x
Wang, C., Wu, H., Zhu, B., Song, J., Lu, T., Li, Y. Y., & Niu, Q. (2020). Investigation of the process stability of different anammox configurations and assessment of the simulation validity of various anammox-based kinetic models.RSC Advances, 10(64), 39171-39186. https://doi.org/10.1039/D0RA06813F